「キングズベリーの怪異」シーン関係図
「キングズベリーの怪異」は『トレイル・オブ・クトゥルー』のルールブックに掲載されているシナリオです。
ルールブックに載ってるぐらいなので入門用のシナリオのはずですが、いやいや、これそこそこ経験のあるGM/KPじゃないと迷子になるよ?というマスタリング難易度です。
その分、『トレイル・オブ・クトゥルー』らしさは味わえると思います。おそらく『クトゥルフ神話TRPG』経験者を想定しているのでしょう。
さて、以下が「キングズベリーの怪異」のシーン関係図(Scene Flow Diagram)になります。
これは「このシーンからこのシーンへ移動する」というよりも、「このシーンで核心的手がかりを見つけると、次のシーンへ行けるようになる」という関係を示しています。
前半の脇道の多さと二つの自由裁量型シーンの扱い方が難しいところです。
続きを読むGUMSHOE SRD CREATIVE COMMONS VERSION の抄訳
GUMSHOE SRD CREATIVE COMMONS VERSION (Version3) の Designing Scenarios (シナリオをデザインする)の項目を訳出してみました。
GUMSHOE SRDは Creative Commons 3.0 Attribution Unported Licenseで公開されています。
最近、『トレイル・オブ・クトゥルー』(ToC)というTRPGにハマってます。
これは大人気のTRPG『クトゥルフ神話TRPG』(CoC)をお手本にしつつ、より調査探索を楽しめるようにしたシステムです。
『クトゥルフ神話TRPG』がBRP(Basic Role-Playing)システムを根幹として作られているのと同様に、『トレイル・オブ・クトゥルー』はGUMSHOEシステムに基づいて作られています。
このGUMSHOEシステムはCC BY 3.0 で公開されているので、その一部を翻訳してみました。(もっとも、ほぼほぼDeepL頼りですが。)
このDesigning Scenarios (シナリオをデザインする)の項目は『トレイル・オブ・クトゥルー』や『(新)クトゥルフ神話TRPG』のシナリオを書く際やマスタリングの参考になると思います。
シナリオをデザインする
GUMSHOEのシステムは、ある種のシナリオ・デザインに対応しています。ゲームの成功にとって、ルールはそれほど重要ではなく、冒険をどのように構成するかということが重要なのです。
手がかり
物語を進めるために必要不可欠な情報があれば、それは核心的手がかりとなります。コストはかかりません。また、ポイントを消費するほど重要でない情報であれば、0ポイントで小ネタを提供することができます。
行動の脇役として楽しいが、物語を進めるのに必須ではない情報がある場合、1ポイントまたは2ポイントを消費して利用できるようにします。ゲーム世界での難易度ではなく、その情報の娯楽的価値に応じて消費コストを選択します。このシステムのポイントは、手がかりを簡単に入手できるようにし、プレイヤーはその手がかりがどのように組み合わされるのかを考えるのを楽しめるようにすることです。そのためには、情報が手に入りやすいような選択をすることが大切です。習慣はなかなかなくならないので、古いパラダイムに逆戻りして、手がかりを得にくくすることのないようにしてください。
ある行動が失敗したときの結果が狂気や死や怪我であるならば、ぜひとも判定をしましょう。ゲーム世界の論理から、脇役のキャラクターが積極的にキャラクターに対抗してくるようであれば、それを対抗判定にしましょう。
手がかりの種類
特殊な手掛かりの種類は以下の通りです。
自由裁量型核心的手がかり
シナリオを構成する上で、1つ以上の自由裁量型核心的手掛かりを用意すると便利な場合があります。これらは通常、物語をある明確なセクションから別のセクションへと進めるものです。通常の核心的手がかりが特定のシーンと結びついているのに対して、自由裁量型手掛かりはいくつかのシーンのどれからでも得ることができます。GMはプレイ中に、どのシーンで手がかりを得るかを決定します。
自由裁量型核心的手がかりは、シナリオのテンポを調整することができます。これにより、キャラクターはシナリオのある部分で楽しい経験や興味深い経験をすべてした後、物語が劇的な展開を見せるようになります。例えば、エソテロの容疑者全員と別々に会ってから、彼らや探索者を古い暗い家に一晩閉じ込めてしまいたいとします。そのためには、探索者たちを暗い家へ向かわせる核心的手がかりを、関連する脇役たちに全員会った後まで伏せておくのです。そうすることで、この後の展開を楽しむために必要な情報を得られないまま、物語が先走りしてしまうことを防ぐことができます。
同様に、自由裁量型手がかりがあれば、物語を盛り上げたいときに不要なシーンをスキップすることができ、冷酷な編集者のような役割を果たすことができるのです。例えば、探索者が論理的に必要な手がかりを得る可能性のあるシーンを5つ選んだとしましょう。この段階には1時間程度かかるとします。もしプレイヤーが各シーンを10分ずつで駆け抜けるなら、核心的手がかりは最後のシーンまで取っておくことができます。もしプレイヤーが1シーン20分もかかるようなら、3シーン目以降で核心的手がかりを入手できるようにした方がよいでしょう。
制限時間よりも、プレイヤーのフラストレーションの方が、核心的手がかりを浮かせるきっかけになることが多いです。もし、あなたが作った生き生きとした脇役とのやりとりを明らかに楽しんでいたり、不気味な現象にゾクゾクしているのなら、最後のシーンまで核心的手がかりを取っておくことで、彼らが望むものをより多く与えることができます。逆に、退屈でイライラしているようであれば、早めに自由裁量型手がかりを入れるのも手です。
梃入れする手がかり
ミステリー小説の定番といえば、それまで抵抗していた目撃者や容疑者に決定的な事実を提示することで、刑事が求めていた情報や自白を突然提供し、その結果、その人物が折れてしまうというものです。これをGUMSHOEでは、梃入れする手がかりとして表現しています。これは、ある交渉系探索技能を使って、以前に集めた別の手がかりに言及することで、初めて得られる情報です。引用された手がかりは前提手がかりと呼ばれ、定義上、核心手がかりの下位カテゴリに位置づけらます。
パイプ手がかり
謎を解くのに重要な手がかりのうち、シナリオのずっと後になって重要になる手がかりをパイプ手がかりと呼びます。これは脚本家の専門用語で、シナリオの後半に関連する説明を挿入することを「パイプを敷く」と表現します。この言葉は、物語の情報を注意深く配置することを、家を建てる配管工の仕事になぞらえています。
パイプ手がかりは、シナリオに構造的な変化をもたらし、キャラクターがシーンAからシーンB、シーンCへと一直線に誘導される感覚を和らげます。パイプ手がかりのリスクは、プレイヤーの記憶が弱くなることである。特に数回のセッションを重ねるうちに、プレイヤーの記憶力が低下する可能性があります。
制限された手がかり
謎の解決に必要な手がかりの中には、それを入手するために必要な探索技能を持つ誰もが知っているわけではないものがあります。その代わりに、あるグループのメンバーが偶然知っている秘密や難解な事実、あるいは曖昧な事実が制限された手がかりとなります。
コーンウォリス作戦を知る者は限られているが、捜査に必要であれば、探索者もその一人でしょう。
また、「あまり知られていない事実を知っている」という感覚を大切にするため、その情報を知っているのはグループのメンバー1人だけで、他の探索者には、同じ探索技能を持つ者でも、その情報はニュースとして伝わります。関連する探索技能を持つキャラクターが、手がかりとなる行動を最初に取ることで、この偶然の知識に恵まれる。探索者が現場に入ってすぐに与えられる手がかりのように、明確な最初の行動者が存在しない場合、GMはその探索技能の現在のプール値が最も高い探索者(該当する場合)、またはスポットライトがあたる時間が最も短い探索者、または幸運の逆転を最も必要とする探索者を選択する。例えば、《官僚制度》が高いキャラクターは、エソテロの容疑者を裏方の仕事から見抜くことができるかもしれません。
時間差のある結果
以下の構造的テクニックは、登場人物が科学捜査研究所のサービスを利用し、他の人が行った判定に依存するGUMSHOEのゲームに適用されます。時間差のある結果で、事件のテンポを形成することができます。これは、科学捜査の専門家に証拠を提出してから、彼らが行う判定の結果が出るまでの間に、信憑性を高めるために適切な間隔が必要な場合に発生します。警察の手続きでは、検査結果が出たときに捜査の方向性が突然変わることはよくあることです。科学的な証拠は、現在の第一容疑者の容疑を晴らすかもしれないし、新しい目撃者や場所に捜査当局を向かわせるかもしれない。 あるいは、以前に得た情報の意味が変わり、捜査官が以前の目撃者に再聴取を行ったり、犯罪現場をより詳しく調べたりすることになる場合もあります。
時間差のある結果は、遅効性の核心的手がかりとなり、キャラクターを新しい現場に向かわせることができます。これらは、各場面がどのような順番でつながっていてもよい場合に有効な装置です。もし、キャラクターがあるシーンで退屈したり、つまづいたりしているときに、研究所から電話がかかってきて、必要な説明を受け、新しい方向へ進むことができます。また、時間差のある結果の到着は、新しいシーンに移動することなく、現在の事件メモに対するプレイヤーの解釈を変えることができます。容疑者のアリバイを否定したり、事件の時間軸を変更したり、目撃者の証言が信頼できないことが判明して、その情報を否定したりすることもあります。
また、研究所の報告書に関するニュースを利用すれば、手がかりをすべて集めたにもかかわらず、プレイヤーが見捨てないようなシーンを切り上げることもできる。
記録はあなたの味方
アドベンチャーノートの他に、ゲーム運営に必要な資料が2つあります。アドベンチャーを作成する際に、探索技能チェックリストに使用した探索技能をメモしておきます。なるべく幅広い探索技能の手がかりを加えておくとよいでしょう。また、キャラクター作成時にチェックリストを使って、すべての探索技能が網羅されているか、冗長な探索技能は省かれているかを確認することもできます。
次に、キャラクター作成時に、プレイヤーに探索技能の選択をGMの探索者名簿に書き込んでもらいます。これにより、どのキャラクターが明らかな手がかりに気づきそうか、スポットライトを浴びる時間が均等になるかを選ぶことができます。
次のセッションを準備するとき、探索者名簿を使って、プレイヤーたちが何に興味を持つかを確認することができます。誰かが《美術史》で3点を持っていれば、贋作や脅威的な彫刻をメモに追加することができます。これは即興のゲームでは特に有効です。
シーンの種類
謎の構想ができたら、次はそれをシーンにアレンジしていきます。それぞれのシーンは、異なる場所で行われるか、異なる脇役との対話が行われます(通常はその両方)。シーンのタイトルの下には、シーンの種類と、現在のシーンにつながるシーンと、そこからつながるシーンを書きます。以下は、入門アドベンチャーのシーンヘッダーの例です。
善良な牧師
シーンタイプ: 核心
リードイン: ブリーフィング
リードアウト: 幻視者、懐疑論者、セコイア市のニューシャウンド
シーンは以下のタイプに分類されます。
導入
このエピソードの最初のシーンです。謎の前提を確立します。登場人物の初対面であれば、まず探索者同士が出会えるようにします。そして、ベリティ氏と安全な場所で会い、そこでブリーフィングを行い、質問に答えます。すでにある緊急事態に対処するために派遣された場合は、直接現場に行き、そこでベリティ氏からブリーフィングを受けます。『the Esoterrorists』の初回セッションであれば、このシーンを延長することができます。預言者ブンコ作戦*1の導入シーンを参照してください。
核心
核心となるシーンでは、調査を完了し、クライマックス・シーンに到達するために必要な情報が少なくとも1つ提示されます。
各核心シーンには、少なくとも1つの核心的手がかりが必要です。
核心的手がかりは、通常、他のシーン(多くの場合、核心シーン)へ導きます。
一対一で結びつけられた核心的な手がかりは避けてください。単一の順序でしか互いに導くことができません。
あなたは、物語を通して別の核心的手がかりに移動するための方法の一つを構築しているのであって、唯一の方法ではないのです。プレイ中、あるシーンの核心的手がかりを、プレイヤーの論理的な行動から着想を得た即興の別のシーンに配置することがあります。(シーン構成は、少なくとも1つの方法で物語を進めることを保証するものであり、他の順序でシーンを進めること排除するものではありません。)また、シーン構成に従うことで、プレイヤーの選択によって物語が分岐していくことも保証されます。これにより、脇役の行動によって物語が進行し、プレイヤーは多かれ少なかれ受動的にそれを観察する、という事態を避けることができます。
情報の配置
核心シーンには、核心的手がかりの他に、多くの情報が含まれているのが一般的です。情報は理解や文脈を与えてくれるかもしれません。あるいは、無関係な細部に注意が行ってしまい、謎が不明瞭になることもあります。シーンの作成は、プレイヤーの質問を予測し、その質問に答えることです。
登場人物の専門家である探索者が、どのような答えを出すべきかを考えること。
核心的でない手がかりをすべて消費しないこと。以下の場合に核心的でない手掛かりを追加する。
- 楽しくて難解な事実を思いついたとき。
- 関連性のない、または不明瞭な情報 。
- レーザーは、他の方法よりも早く情報を得ることができるかもしれません。
- その他の実用的な利点を確保できるかもしれない
消費することによって、ポイントを与えるキャラクターがより印象的になるか、他の利点が得られるのでなければ、それは消費すべきではありません*2。
置き換え
置き換えシーンは、中心的な謎を理解し解決するのに役立つ情報を提供しますが、結論に到達するために厳密には必要ではありません。多くの場合、文脈や詳細を提供します。あるいは、核心シーンと同じ情報を、別の方法で提供することもある。第三の選択肢として、赤信号の可能性を排除することができるかもしれない。これらの免責的事実は貴重であり、厳密には別の核心的手がかりにつながらないにもかかわらず、レーザーが本当の答えへと探索を絞り込むことを可能にします。
敵役の反応
危険やトラブルが発生し、グループの成功に反対するサポートキャラクターが、グループを阻止したり、後退させるために行動を起こすシーンです。これは戦闘シーンかもしれませんが、政治的な問題や妨害行為など、直接的でない挑戦もありえます。もし記録を取るのに役立つなら、直面した敵が主要な敵ではなく、付随的な敵であることを括弧書きで記すとよいでしょう。敵役の反応は自由裁量型にすることができます。つまり、事態が停滞しているときにペースを上げるために利用することができます。
危機
危機シーンでは、グループの安全や調査の継続を妨げる非人間的な障害物が提示されます。通常、判定や対抗判定を通じて克服する必要があります。
サブプロット
サブプロットのシーンでは、捜査の流れを直接変えることなく、登場人物たちが自由に行動し、取引し、探索し、交流する機会が与えられます。小ネタは、個人的な周辺、裏取引、広報活動、あるいは単に1人または複数の探索者の好奇心などから発生することがあります。中心的な謎が構成と推進力を提供する一方で、サブプロットは味わいと個性を加えます。 サブプロットから発生する流れは、謎が一段落した後でも、グループの記憶に残るかもしれません。サブプロットは、長期的なキャンペーンプレイに適しています。
結末
結末は、グループに捜査の終わりをもたらし、しばしば道徳的ジレンマ、物理的障害、またはその両方に直面させます。機能的には、最後の危険や敵役の反応シーンですが、プレイヤーがエソテロリストやODEに突入することによって始まる場合もあります。古典的な RPGの謎の結末は大乱闘です。あなたのグループは、クライマックスの喧嘩にこだわるかもしれませんし、早口と巧妙な思考でそれを回避することを好むかもしれません。戦闘やその他のアクションシーンを、エキサイティングで決定的なものにするのは簡単なことです。『The Esoterrorists』では、結論は血なまぐさく、正気を脅かすものになりがちです。
混合シーン
一般的な課題から情報提供のチャンスにつながるような、二度おいしいシーンもあります。障害を克服した報酬として核となる手がかりを与えるのは、その核心的手がかりが他の手段でも得られる場合のみでよいでしょう。そうでない場合、核心的手がかりが手に入らないという事態を招き、GUMSHOEシステムの基本的な考え方に反することになります。
シーン関係図
プレイヤーの選択がシナリオに重要であることを確認するために、シナリオのシーンを図解してみましょう。矢印で結び、どのような順番でも解けることを確認します。調査以外のシーン(敵役の反応、危機、サブプロット)で予測不可能性や多様性を加えることは許容されますが、プレイヤーが核心シーンと置き換えシーンを複数の方法で接続できるようにするとより良い形になります。
プレイヤーの活性化
捜査シナリオに対するよくある不満は、プレーヤーが決められたストーリーの道筋に忠実に従うよう「レールを敷かれる」ことです。このような苦情はほとんど見られませんが、方向性が定まっていないと、多くのグループが混乱に陥ります。
議論が活発で楽しそうである限り、プレイヤーに選択肢を考えさせましょう。もし、グループがイライラして、まとまった選択ができないようなら、そっと話し合いに割って入ってください。様々な提案をまとめ、議論に結論を出すように仕向けましょう。好ましい答えに誘導することなく、プレイヤーが選択肢を排除できるよう導いてください。このような冷静さは、1つに決めない方が達成しやすいのです。
ミステリーシナリオで前進する唯一の方法は、より多くの情報を収集することであることをプレイヤーに思い出させましょう。事態が停滞しているときは、登場人物の行動を参照します。目の前にある選択肢の中で、どの選択肢が最も自分の原動力に適しているかを尋ねてみましょう。
選択肢が多すぎて選べない、あるいは明らかにリスクのない選択肢がないために、プレイヤーが圧倒されそうになる場合も想定しておきます。そのようなときは、自分の衝動を呼び起こし、前に進むように促します。彼らがOVによって問題解決者として訓練されてきたことを思い出させます。おそらくプレイヤーとは異なり、キャラクターは仮説を立て、情報を集めてそれを検証し、理論を修正し、前に進むことに慣れています。ジレンマがあっても、それをステップに分解して対応します。少し指導すれば、この問題解決の方法論はすぐに身につくでしょう。プレイヤーは、決められたシナリオをこなすことで鍛えられた「手がかりを待つ」受動性を捨て、自ら率先して行動することを学ぶでしょう。
否定を避ける
ミステリーシナリオを運営する場合、プレイヤーの2~3シーン先を考えるのが有効です。 また、クライマックスの流れも考えておくと便利なことが多いです。そうすることで、その前のシーンから論理的に発展したエンディングに見えるよう、十分な伏線を張ることができるのです。(これについては、次のセクションを参照してください)。
このとき、思い描いた分岐点を固定化しすぎないようにしましょう。 むしろ、仮のものにしておいて、そこから離れて、よりプレイヤーの意見に沿った新しい選択肢に代えることができるようにしましょう。
これは、舞台俳優が使う即興の基本原則を言い直したもので、決して否定してはいけないということです。寸劇が展開する中で、一人の演者がもう一人の演者を母親と認識した場合、もう一人の演者はその選択を受け入れ、それを土台にしなければなりません。そのとき、「私はあなたの母親ではありません」と簡単に否定してしまうのは、非常にまずいやり方です。それは、物語を止めてしまい、それを進めようとした他の参加者を罰することになるからです。
同じように、予想外の可能性を受け入れ、それを進行中の物語に組み込むことで、予想外の可能性に対応できるように訓練しましょう。例えば、病理学者のエルザ・ハワーは、新鮮な死体を必要とするエソテロの計画に巻き込まれた無実のカモだと判断したかもしれない。しかし、プレイヤーが彼女を悪役と見なすことを強く望んでいるのであれば、その予定された事実を脇に置いて、彼女を裁いたときに無上の勝利感を味わえるようにすることを考えるかもしれません。
プレイヤーの指示をすべて額面通りに受け入れる必要はありません。取り入れた要素にひねりを加えて、物語に驚きを与え続けましょう。迷ったら、プレイヤーの半分くらいを正解にする。おそらくエルザはODEに寄生されており、それを取り出して感情的に満足のいく報いを受けさせることで、チームは無実の人を救うと同時に罪人を罰することができるのです。
プレイヤーからのインプットのたびに、物語を急展開させる必要はないのです。重要なのは、何も起こらないシーンや、プレイヤーが提案したシーンより自分のシーンの方が面白くないという事態を避けることです。プレイヤーが「廃墟の城塞にあるコンピューター・アーカイブにはホログラフィック・ライブラリーがあるはずだ」と言ったとき、それを除外したり、プレイヤーがそこから消費するのに適した探索技能を持っていないために見つけることができないようにするのは、残念なことです。ホロキャラクターから有用な情報を引き出すことは、そうしないよりも楽しいし、よりプロットを進展させます。しかし、これはプログラムがその後で厄介な驚きを与えてはいけないということを意味するものではありません。
リードとフォロー
即興はテクニックであり、最終目的ではありません。時には、あなたが物語の手綱を握って、特定の方向に誘導した方が、関係者全員を楽しませることができる場合もあります。これは、シナリオの終盤で、すべての物語を首尾一貫した満足のいく結末にまとめようとするときに起こりがちなことです。
これもまた、プレイヤーの気分や態度に対応する問題です。プレイヤーが積極的に物語に参加し、楽しい提案を投げかけているときは、彼らのリードに従いましょう。彼らの創造性が壁にぶつかったら、それを拾ってあげましょう。即興は、ギブアンドテイクの有機的なプロセスなのです。
以上です。
複数回答(multiple answer, MA)の集計表をコレスポンデンス分析にかけて大丈夫?
複数回答(multiple answer, MA)の集計表をコレスポンデンス分析にかけて大丈夫?
結論から言うと、大きな問題はなさそうです。
複数回答とは?
ブランドのイメージなどを聞くアンケートでは、「○○ブランドのイメージとして、あてはまるものをすべて選んでください」というような設問がよく使われます。
1つの設問に対して、複数の選択肢を選ぶことができる形式で、複数回答(multiple answer)、略してMAとも呼ばれます。
MAのコレポン問題
このタイプの質問の分析にはコレスポンデンス分析がよく使われます。
コレスポンデンス分析には集計表の周辺度数をかけ合わせた期待値が使われますが、複数回答の場合周辺度数が100%にはならない(回答者数が100%)ので、そのままコレポンにかけるのはマズいのでは???というのが実は長年の疑問でした。
そこで、こんなふうに考えてみました。
複数回答は、各選択肢毎単数回答(single answer)をまとめたものと解釈できる。
それであれば、各選択肢毎に選択、非選択の両方をカウントしたクロス集計表をもとにコレポンすれば問題ないんじゃないか?
検証してみる
検証のためのデータとして、GMOリサーチさんのデータを引用させていただきます。
「n=100」との記載がありますが、各セグメントごとにn=100と解釈しました。
library(tidyverse) library(ggrepel) ##### データ整形 dat_MA <- matrix( c( 13, 13, 8, 23, 16, 20, 3, 4, 25, 13, 8, 23, 8, 10, 8, 5, 28, 6, 7, 25, 7, 15, 5, 5, 7, 8, 6, 38, 12, 21, 4, 4, 8, 12, 24, 10, 9, 7, 28, 2, 12, 20, 17, 18, 7, 6, 10, 10, 15, 21, 19, 15, 4, 12, 4, 10, 5, 9, 10, 29, 17, 19, 8, 3 ), ncol = 8, byrow = TRUE, dimnames = list( 性年代 = c( "20代男性", "30代男性", "40代男性", "50代男性", "20代女性", "30代女性", "40代女性", "50代女性" ), コンビニで買うお昼ご飯 = c( "おにぎり類", "パン類", "サンドイッチ", "弁当類", "パスタ類", "ラーメン・うどん類", "野菜・サラダ類", "冷凍食品類" ) ) ) dat_SA <- cbind( dat_MA, 100 - dat_MA ) dimnames(dat_SA)[[2]] <- c( paste0("y_", dimnames(dat_MA)[[2]]), paste0("n_", dimnames(dat_MA)[[2]]) ) dat_SA
これで各選択肢の選択(y)、非選択(n)をまとめたクロス集計表ができました。
コレポンする
従来の選択項目のみをカウントした集計表と、選択、非選択をまとめたクロス集計表を、それぞれコレスポンデンス分析にかけ、比較してみます。
library(ca) res.ca_MA <- ca(dat_MA) # 選択項目のみの従来型 res.ca_SA <- ca(dat_SA) # 選択、非選択をまとめたSA型 summary(res.ca_MA) summary(res.ca_SA) res.plot.ca_MA <- plot(res.ca_MA, main = "MA", map = "symbiplot", arrows = c(TRUE, TRUE)) res.plot.ca_SA <- plot(res.ca_SA, main = "SA", map = "symbiplot", arrows = c(TRUE, TRUE))
行要素の比較
MAとSAの行要素について、コレポンの結果を比較してみます。
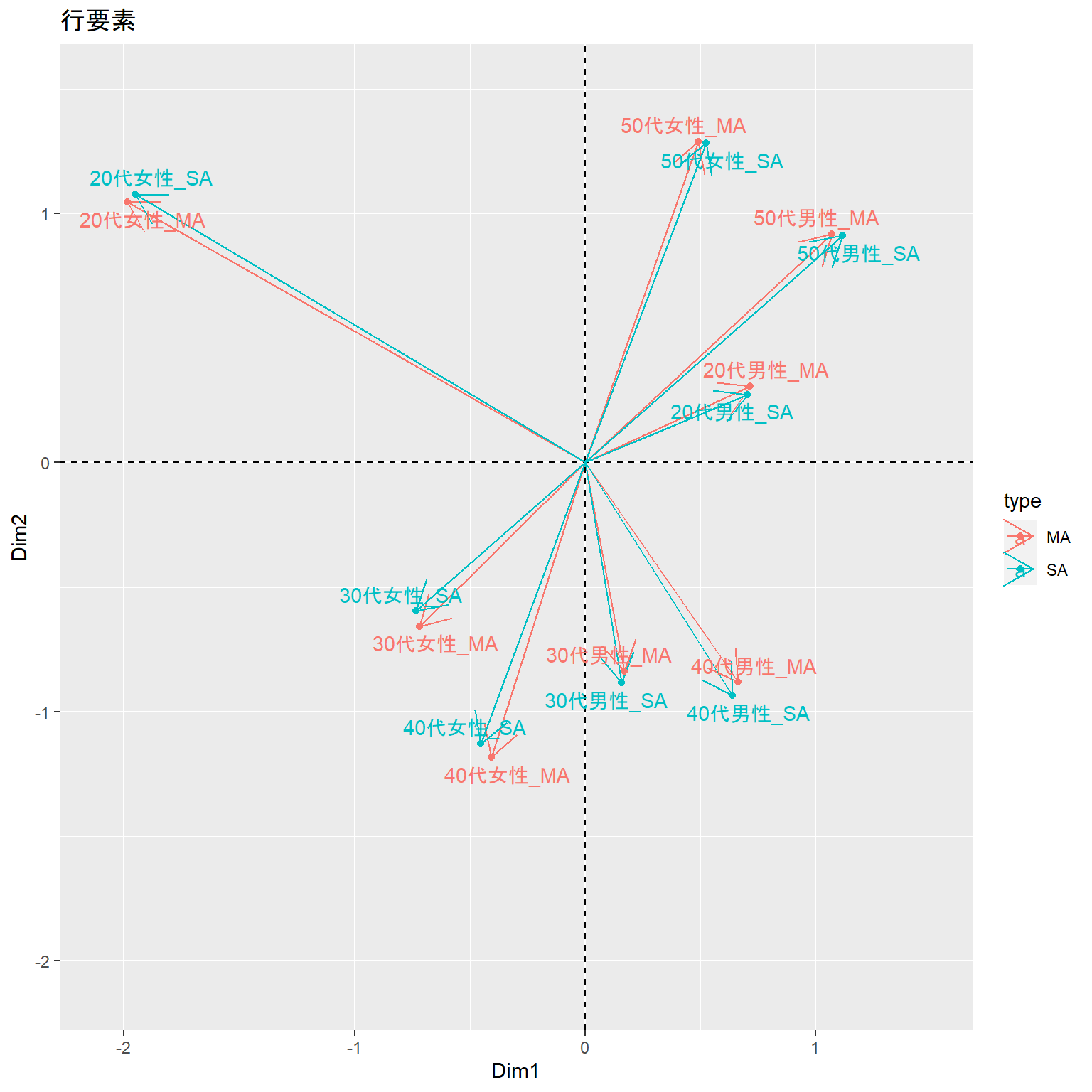
微妙にずれますが、ほぼ同じと解釈してもよさそうです。
res.plot.ca_MA$rows %>% as.data.frame() %>% rownames_to_column() %>% mutate( rowname = paste0(rowname, "_MA"), Dim1 = scale(Dim1), Dim2 = scale(Dim2), type = "MA" ) %>% bind_rows( res.plot.ca_SA$rows %>% as.data.frame() %>% rownames_to_column() %>% mutate( rowname = paste0(rowname, "_SA"), Dim1 = scale(Dim1), Dim2 = scale(0 - Dim2), #x軸を反転 type = "SA" ) ) %>% ggplot(aes(x=Dim1, y=Dim2, label = rowname, color=type)) + scale_x_continuous(limits = c(-2.1, 1.5)) + scale_y_continuous(limits = c(-2.1, 1.5)) + geom_hline(yintercept = 0, linetype = 2) + geom_vline(xintercept = 0, linetype = 2) + geom_segment(aes(x=0, y=0, xend=Dim1, yend=Dim2), arrow = arrow(type = "open")) + geom_point() + geom_text_repel() + labs(title = "行要素")
列要素の比較
こんどは列要素について、比較してみます。

こちらも微妙にずれますが、ほぼ同じと解釈してもよさそうです。
# 列要素 ほぼ一致 res.plot.ca_MA$cols %>% as.data.frame() %>% rownames_to_column() %>% mutate( rowname = paste0(rowname, "_MA"), Dim1 = scale(Dim1), Dim2 = scale(Dim2), type = "MA" ) %>% bind_rows( res.plot.ca_SA$cols %>% as.data.frame() %>% rownames_to_column() %>% slice(1:8) %>% mutate( rowname = paste0(rowname, "_SA"), Dim1 = scale(Dim1), Dim2 = scale(0 - Dim2), #x軸を反転 type = "SA" ) ) %>% ggplot(aes(x=Dim1, y=Dim2, label = rowname, color=type)) + scale_x_continuous(limits = c(-2, 1.25)) + scale_y_continuous(limits = c(-2, 1.25)) + geom_hline(yintercept = 0, linetype = 2) + geom_vline(xintercept = 0, linetype = 2) + geom_segment(aes(x=0, y=0, xend=Dim1, yend=Dim2), arrow = arrow(type = "open")) + geom_point() + geom_text_repel() + labs(title = "列要素")
結論
ということで、MAの集計表をそのままコレポンにかけても実用上は問題なさそうです。
R上のデータフレームをDBにテーブルとして書き込む
Tokyo.Rで質問があったので。
# R上のデータフレームをDBに書き込む方法 library(RSQLite) library(nycflights13) #サンプルデータ # サンプルデータの確認 # これらのデータフレームをDBにテーブルとして書き込む head(airlines) head(airports) head(flights) head(planes) head(weather) # 空のDBを作る、もしくは既存のDBにつなげる conn <- dbConnect(SQLite(), "nycflights13.db", synchronous="off") # DBにDFをテーブルとして書き込む # dbWriteTable(コネクション, "新たに作るテーブル名", 書き込みたいデータフレーム) dbWriteTable(conn, "Airlines", airlines) dbWriteTable(conn, "Airports", airports) dbWriteTable(conn, "Flights", flights) dbWriteTable(conn, "Planes", planes) dbWriteTable(conn, "Weather", weather) # 書き込めたか、DBのテーブルを確認 dbListTables(conn) # テーブルのフィールド名を確認 dbListFields(conn, "Airports") # 接続を切る dbDisconnect(conn)
コレスポンデンス分析の同時布置図は本当に使えないのか?(点と点の距離の話)
前回、前々回のコレスポンデンス分析についての話を目にした何人かから、「そもそもコレポンの同時布置図を点の距離で解釈しちゃいけないなんて聞いてない。どうしてダメなのか教えてほしい。」という声をいただきました。
「どうしてダメなのか?」を数学的に説明するのは私には無理なので、朝野先生による解説などを参照していただきたいです。
今回は「実際、コレポンの同時布置図では点の距離で行と列の関係を表現できていないのでダメです。」という話をします。
サンプルデータは前回も使った日経リサーチさんのデータを引用させていただきます。
dat <- c( 18, 43, 175, 249, 52, 133, 78, 34, 93, 40, 207, 165, 108, 35, 78, 23, 115, 97, 30, 52, 124, 248, 59, 29, 48, 19, 113, 75, 165, 161, 24, 25, 47, 177, 36, 126, 16, 38, 21, 11, 36, 48, 101, 97, 86, 63, 50, 57, 50, 54, 58, 35, 43, 63, 42, 45, 37, 53, 32, 49, 51, 284, 26, 15, 7, 6, 52, 11, 110, 144, 10, 17, 27, 118, 20, 87, 8, 9, 4, 10, 284, 7, 452, 188, 76, 25, 177, 223, 181, 19, 156, 39, 272, 86, 52, 85, 28, 85, 185, 318, 60, 2, 265, 100, 72, 55, 64, 66, 33, 10, 115, 45, 111, 20, 32, 12, 39, 48, 62, 123, 85, 4, 329, 132, 79, 51, 94, 105, 67, 27, 118, 32, 121, 47, 32, 42, 25, 72, 94, 182, 189, 40, 233, 36, 27, 16, 80, 176, 107, 19, 57, 24, 88, 73, 13, 67, 7, 49, 89, 104, 106, 112, 87, 20, 16, 11, 63, 60, 55, 65, 24, 10, 43, 69, 10, 43, 8, 31, 38, 26, 37, 297, 31, 23, 14, 14, 60, 20, 102, 94, 24, 14, 19, 87, 26, 71, 4, 21, 6, 10, 148, 28, 197, 46, 25, 21, 70, 151, 80, 10, 78, 22, 67, 55, 16, 53, 12, 43, 73, 73, 77, 100, 159, 81, 32, 26, 118, 125, 126, 22, 110, 25, 81, 77, 29, 78, 15, 79, 48, 45, 352, 40, 253, 18, 24, 13, 125, 203, 164, 111, 30, 22, 177, 184, 12, 98, 14, 79, 119, 152, 24, 240, 58, 120, 44, 117, 95, 18, 125, 87, 76, 88, 69, 55, 96, 67, 161, 61, 17, 24, 42, 16, 149, 42, 41, 38, 30, 37, 13, 8, 58, 30, 49, 18, 10, 12, 28, 29, 28, 43, 168, 121, 140, 75, 50, 35, 140, 97, 184, 98, 39, 25, 88, 157, 30, 153, 57, 68, 64, 77, 72, 155, 106, 43, 25, 27, 64, 42, 113, 59, 49, 19, 48, 77, 13, 71, 18, 48, 39, 36, 49, 155, 74, 24, 34, 27, 59, 35, 64, 63, 27, 17, 28, 66, 20, 47, 18, 30, 23, 18 ) |> matrix( nrow = 18, byrow = TRUE, dimnames = list( Brands = LETTERS[1:18], Attributes = c( "伝統や格式を重んじる", "庶民的", "価格が高い", "流行を作り出している", "価値上昇", "新鮮味", "顧客の心つかんでいる", "気品を感じさせる", "ファン層幅広い", "機能性重視", "デザイン重視", "既成概念囚れない", "存在感", "ずっと付合っていける", "社会動きに敏感", "誰からも好かれる", "躍動感", "さりげなく特徴をアピール", "豊かな気持ちにさせる", "自慢になる" ) ) )
まず、コレスポンデンス分析で表そうとしている行と列の関係はクロス集計表の残差であるとします。
残差は実測値と期待値との差であり、期待値通りでない部分に行と列の関係が現れます。
ただ、この残差はサンプルサイズの影響を受けるので、何らかの方法で標準化する必要があります。
これが指標化残差です。
n <- sum(dat) # 総度数(n) P <- dat/n # 観測割合(P) row.masses <- rowSums(P) # 行質量(row masses、平均列プロファイル) column.masses <- colSums(P) # 列質量(column masses) E <- row.masses %o% column.masses # 期待値 R <- P - E # 残差 I <- R / E # 指標化残差
この指標化残差が同時布置図上で行の点と列の点の距離として表現できていればいいはずです。
確認してみましょう。
まずはコレスポンデンス分析を実行し、同時布置図上の座標を取得します。フレンチプロット、非対称プロット、対称バイプロットの3パターンで確認します。
library(ca) res.ca <- ca(dat) map_symm <- plot(res.ca, map = "symmetric") map_rowpr <- plot(res.ca, map = "rowprincipal") map_symbi <- plot(res.ca, map = "symbiplot")
行の点と列の点の距離はdist()関数で取得できます。
dist_symm <- rbind(map_symm$rows, map_symm$cols) |> dist() vec_symm <- as.matrix(dist_symm)[1:18, 19:38] |> as.vector() dist_rowpr <- rbind(map_rowpr$rows, map_rowpr$cols) |> dist() vec_rowpr <- as.matrix(dist_rowpr)[1:18, 19:38] |> as.vector() dist_symbi <- rbind(map_symbi$rows, map_symbi$cols) |> dist() vec_symbi <- as.matrix(dist_symbi)[1:18, 19:38] |> as.vector()
あとは、指標化残差とこれらの距離の関係を散布図で確認します。 何らかの比例関係が認められれば、距離で指標化残差が表現できているといえるはずです。
Iv <- I |> as.vector() par(mfrow=c(2,2)) plot(Iv, vec_symm, main="フレンチプロット", pch=21, col = "#0000ff", bg="#0000ff33", xlab="標準化残差", ylab="行の点と列の点の距離") plot(Iv, vec_rowpr, main="非対称プロット", pch=21, col = "#0000ff", bg="#0000ff33", xlab="標準化残差", ylab="行の点と列の点の距離") plot(Iv, vec_symbi, main="対称バイプロット", pch=21, col = "#0000ff", bg="#0000ff33", xlab="標準化残差", ylab="行の点と列の点の距離")

一定の相関はあるものの、やはり距離で行と列の関係を表せているとはいいがたいようです。
というわけで、コレポンの同時布置図における行と列の関係は、距離ではなく、角度(方向)と長さで解釈した方が良いようです
コレスポンデンス分析の同時布置図は本当に使えないのか?(の続き)
前回の記事の続きです。 bob3.hatenablog.com
- 結論
- 使える同時布置図の描き方
- コレスポンデンス分析の基本的な流れ
- 標準化残差の算出
- 標準化残差(Z)を特異値分解する
- ちょっと脱線 カイ二乗検定と残差分析
- 座標の重みづけ
- 座標の組み合わせ
- 指標化残差が角度と長さで表現できてるか確認
- 大きな集計表で再確認
- 結論(再掲)
- 参考リンク
結論
今回も最初に結論を。
- 縦横のスケールを合わせるのが大前提です。
- そうしないと見かけ上の角度が歪んでしまいます。
- コレスポンデンス分析の同時布置図を描くときは、対称バイプロットがおすすめです。
- 指標化残差を正確に角度として表現できて、なおかつ見やすいので。
- 従来の同時布置図はフレンチプロットが多いと思いますが、正確でないのであえて選ぶ理由はないと思います。
- ただ、「だいたい合ってる」ので、角度で読む分には大きく間違えることはなさそう。
なお、tarotanさんの記事も大変勉強になるので参照してください。 tarotan.hatenablog.com
使える同時布置図の描き方
前回の記事では指標化残差を角度で表現したのがコレポンの同時布置図だよ、という説明をしたのですが、肝心の描画に使う座標の作り方は関数任せでした。
今回はいくつかの描画手法について検討し、どれを使えばいいのかを考えてみたいと思います。
まず今回のサンプルデータですが、『対応分析入門』に載っているノルウェイの犯罪統計のデータを引用します。
ミニマムなデータで計算過程を追いたい意図です。
(dat <- c( 395, 2456, 1758, 147, 153, 916, 694, 327, 1347 ) |> matrix( nrow = 3, byrow = TRUE, dimnames = list( 地域 = c("オスロ", "中部", "北部"), 犯罪 = c("強盗", "詐欺", "破壊") ) )) ## 犯罪 ## 地域 強盗 詐欺 破壊 ## オスロ 395 2456 1758 ## 中部 147 153 916 ## 北部 694 327 1347
コレスポンデンス分析の基本的な流れ
以下にコレスポンデンス分析の基本的な計算過程を示します。
- クロス集計表の観測割合(P)を算出する。
- 各セルの値を総度数で割った値。
- 行と列の質量(masses)を算出する。
- 行、列の各カテゴリ毎の観測割合の合計。
- 各セルの期待割合(E)を算出する。
- 行と列の質量をセルごとにかけ合わせた値。
- 行と列に関連が無かった場合に想定される各セルの割合。
- 割合の残差(R)を算出する。
- 各セルの観測割合(P)から期待割合(E)を引いた値。
- 指標化残差(I)を算出する。
- 各セルの割合の残差を期待割合で割った値。
- 標準化残差(Z、ピアソン残差)を算出
- 指標化残差に期待値の平方根を乗じた値。
- (観測値-期待値)/sqrt(期待値)
- 『コレスポンデンス分析の利用法』でいうところの標準化、行と列の純粋な関連性。
- 特異値分解(SVD)で次元縮約。
- 標準化残差(Z)に対してSVDで次元縮約し、2次元のスコアを得る
- 固有値、寄与率もここで算出
- スコアに重みづけを行い同時布置図のための座標を得る。
- 座標の重みづけ
- 標準座標
- 主座標
- 対称バイプロット
- 座標の組み合わせ
- 対称プロット(主座標×主座標)
- 非対称プロット(主座標×標準座標)
- 対称バイプロット
- 座標の重みづけ
1から5までは前回の記事で扱ったのでRのコードを示すにとどめ、今回は6の指標化残差から標準化残差を出すところから始めます
n <- sum(dat) # 総度数(n) P <- dat/n # 観測割合(P) row.masses <- rowSums(P) # 行質量(row masses、平均列プロファイル) column.masses <- colSums(P) # 列質量(column masses) E <- row.masses %o% column.masses # 期待値 R <- P - E # 残差 I <- R / E # 指標化残差 list( `総度数(n)` = n, `観測割合(P)` = P, `行質量(row.masses)` = row.masses, `列質量(column.masses)` = column.masses, `期待値(E)` = E, `残差(R)` = R, `指標化残差(I)` = I ) |> print() ## $`総度数(n)` ## [1] 8193 ## ## $`観測割合(P)` ## 犯罪 ## 地域 強盗 詐欺 破壊 ## オスロ 0.04821189 0.29976809 0.2145734 ## 中部 0.01794215 0.01867448 0.1118028 ## 北部 0.08470646 0.03991212 0.1644086 ## ## $`行質量(row.masses)` ## オスロ 中部 北部 ## 0.5625534 0.1484194 0.2890272 ## ## $`列質量(column.masses)` ## 強盗 詐欺 破壊 ## 0.1508605 0.3583547 0.4907848 ## ## $`期待値(E)` ## 強盗 詐欺 破壊 ## オスロ 0.08486708 0.20159365 0.27609267 ## 中部 0.02239062 0.05318678 0.07284198 ## 北部 0.04360279 0.10357426 0.14185017 ## ## $`残差(R)` ## 犯罪 ## 地域 強盗 詐欺 破壊 ## オスロ -0.036655194 0.09817444 -0.06151925 ## 中部 -0.004448475 -0.03451230 0.03896078 ## 北部 0.041103669 -0.06366214 0.02255847 ## ## $`指標化残差(I)` ## 犯罪 ## 地域 強盗 詐欺 破壊 ## オスロ -0.4319130 0.4869917 -0.2228210 ## 中部 -0.1986758 -0.6488887 0.5348671 ## 北部 0.9426844 -0.6146521 0.1590303
標準化残差の算出
割合の標準化残差(Z、ピアソン残差)は指標化残差(I)に期待値(E)の平方根を乗じることで得られます。
(Z <- I * sqrt(E)) ## 犯罪 ## 地域 強盗 詐欺 破壊 ## オスロ -0.12582469 0.2186553 -0.11708024 ## 中部 -0.02972885 -0.1496484 0.14435664 ## 北部 0.19684458 -0.1978132 0.05989557
標準化残差(Z)を特異値分解する
標準化残差(Z)を特異値分解(singular value decomposition、SVD)に掛け、特異値と特異ベクトルを取り出します。
この特異ベクトルが同時布置図の座標のもとになります。
特異値分解とは何か?の説明は私の手にあまりますので各自で勉強してみてください(すいません……
res.SVD <- svd(Z) # 特異値分解 res.SVD$d # 特異値 ## [1] 4.212385e-01 1.596575e-01 7.558903e-18 U <- res.SVD$u[,1:2] # 左特異行列。行に対応。2次元だけ取り出す。 rownames(U) <- rownames(P) U ## [,1] [,2] ## オスロ -0.6600450 0.04227544 ## 中部 0.3840335 -0.83910599 ## 北部 0.6456461 0.54232272 V <- res.SVD$v[,1:2] # 右特異ベクトル。列に対応。2次元だけ取り出す。 rownames(V) <- colnames(P) V ## [,1] [,2] ## 強盗 0.4717636 0.7915672 ## 詐欺 -0.7822401 0.1724693 ## 破壊 0.4068654 -0.5862387
特異値を二乗したものが固有値になります。割合を出せば寄与率になります。
eigenvalues <- res.SVD$d^2 # 固有値 round(eigenvalues, 4) ## [1] 0.1774 0.0255 0.0000 eigen_prop <- prop.table(eigenvalues) # 寄与率 round(eigen_prop, 4) ## [1] 0.8744 0.1256 0.0000 cumsum(eigen_prop) # 累積寄与率 ## [1] 0.8743891 1.0000000 1.0000000
ちょっと脱線 カイ二乗検定と残差分析
コレスポンデンス分析と良く併用されるカイ二乗検定も、コレスポンデンス分析の計算途中の数値から計算できます。
カイ二乗値は残差の二乗を期待値で割って総度数を掛ければ出ます。
カイ二乗値が出ればp値も計算できます。
(chisq <- sum(R^2 / E * n)) # カイ二乗値 ## [1] 1662.625 pchisq(chisq, (ncol(dat) - 1) * (nrow(dat) - 1), lower.tail=FALSE) # p値 ## [1] 0
ちなみに残差分析の調整済み標準化残差はこう。
(ASR <- Z / sqrt((1 - row.masses) %o% (1 - column.masses)) * sqrt(n)) #調整済み標準化残差 ## 犯罪 ## 地域 強盗 詐欺 破壊 ## オスロ -18.686816 37.35695 -22.453905 ## 中部 -3.164442 -18.32454 19.842422 ## 北部 22.931313 -26.50958 9.010296
調整済み標準化残差からp値を出して、さらに多重比較の調整。
# 残差分析のp値を算出 p.value.matrix <- ASR |> abs() |> pnorm(lower.tail=FALSE) * 2 round(p.value.matrix, 4) ## 犯罪 ## 地域 強盗 詐欺 破壊 ## オスロ 0.0000 0 0 ## 中部 0.0016 0 0 ## 北部 0.0000 0 0 # ホルムの方法による有意水準の調整(多重比較) Dim <- dim(p.value.matrix) p.value.matrix.holm <- matrix(p.adjust(p.value.matrix), Dim[1], Dim[2]) dimnames(p.value.matrix.holm) <- dimnames(dat) round(p.value.matrix.holm, 4) ## 犯罪 ## 地域 強盗 詐欺 破壊 ## オスロ 0.0000 0 0 ## 中部 0.0016 0 0 ## 北部 0.0000 0 0
便利ですね。
座標の重みづけ
ここからが本番です。
特異値分解で得られた特異ベクトルに様々な考え方で重みづけを行い同時布置図を描きます。
同時散布図の描き方には例えば以下のようなものがあります。
| 名前 | 座標 | 行と列の関係 |
|---|---|---|
| 対称プロット(フレンチプロット) | 主座標 | 角度△ |
| 非対称プロット | 主座標と標準座標 | 角度○ |
| 対称バイプロット | 標準座標×特異値の平方根 | 角度○ |
tarotanさんの記事、特に「3. さまざまな座標,さまざまな解釈」の節も参照してください。
ここから座標に重み付けをします。
標準座標
行(または列)のベクトルを行(または列)の質量の平方根で割る。
(standard.coordinates.rows <- sweep(U, 1, sqrt(row.masses), "/")) ## [,1] [,2] ## オスロ -0.8800182 0.05636457 ## 中部 0.9968363 -2.17806838 ## 北部 1.2009506 1.00876133 (standard.coordinates.columns <- sweep(V, 1, sqrt(column.masses), "/")) ## [,1] [,2] ## 強盗 1.2146096 2.0379805 ## 詐欺 -1.3067231 0.2881079 ## 破壊 0.5807713 -0.8368139
主座標
標準座標に特異値を乗じたもの。
(principal.coordinates.rows <- sweep(standard.coordinates.rows, 2, res.SVD$d[1:2], "*")) ## [,1] [,2] ## オスロ -0.3706976 0.008999028 ## 中部 0.4199058 -0.347744988 ## 北部 0.5058866 0.161056329 (principal.coordinates.columns <- sweep(standard.coordinates.columns, 2, res.SVD$d[1:2], "*")) ## [,1] [,2] ## 強盗 0.5116403 0.3253789 ## 詐欺 -0.5504421 0.0459986 ## 破壊 0.2446432 -0.1336036
対称バイプロット
標準座標に特異値の平方根を乗じたもの。
(sympc.coordinates.rows <- sweep(standard.coordinates.rows, 2, sqrt(res.SVD$d[1:2]), "*")) ## [,1] [,2] ## オスロ -0.5711573 0.02252169 ## 中部 0.6469756 -0.87029441 ## 北部 0.7794516 0.40307245 (sympc.coordinates.columns <- sweep(standard.coordinates.columns, 2, sqrt(res.SVD$d[1:2]), "*")) ## [,1] [,2] ## 強盗 0.7883167 0.8143192 ## 詐欺 -0.8481010 0.1151198 ## 破壊 0.3769374 -0.3343671
座標の組み合わせ
これらをもとに、3種類の同時布置図を描いてみましょう。
- 対称プロット(フレンチプロット)
- 非対称プロット
- 対称バイプロット
library(ca) library(factoextra) library(patchwork) res.ca <- ca(dat) p1 <- fviz_ca(res.ca, map = "symmetric", arrows = c(TRUE, TRUE), title="フレンチプロット") + scale_y_continuous(limits = c(-0.6, 0.7)) + scale_x_continuous(limits = c(-0.6, 0.7)) p2 <- fviz_ca(res.ca, map = "colprincipal", arrows = c(TRUE, TRUE), title="非対称プロット(列主座標)") + scale_y_continuous(limits = c(-2.5, 1.5)) + scale_x_continuous(limits = c(-1.75, 2.25)) p3 <- fviz_ca(res.ca, map = "symbiplot",arrows = c(TRUE, TRUE), title="対称バイプロット") + scale_y_continuous(limits = c(-1.0, 1.0)) + scale_x_continuous(limits = c(-1.0, 1.0)) p1 + p2+ p3 + plot_layout(ncol = 3)

非対称プロットでは列が原点近くに集まりすぎてちょっと読み取りにくいですね。
フレンチプロットと対称バイプロットはかなり似ていますが、対称バイプロットの方が縦方向のバラツキが大きくなっています。
指標化残差が角度と長さで表現できてるか確認
問題は指標化残差が角度としてちゃんと反映されているかどうかです。
指標化残差を再確認しておきます。
I ## 犯罪 ## 地域 強盗 詐欺 破壊 ## オスロ -0.4319130 0.4869917 -0.2228210 ## 中部 -0.1986758 -0.6488887 0.5348671 ## 北部 0.9426844 -0.6146521 0.1590303
角度で正しく表現できていれば、行の点Aの座標を(x1, y1)、列の点Bの座標を(x2, y2)とすると、x1 * x2 + y1 * y2が指標化残差と一致するはずです。
一致の度合いは相関係数で確認してみましょう。
フレンチプロット(主座標)
相関係数0.94。一致はしていませんが、「だいたい合ってる」とは言っても良さそう?
COL <- principal.coordinates.columns ROW <- principal.coordinates.rows # ここはもう少し効率的なやり方があるはず…… mat1 <- cbind( ROW[c(1,1,1,2,2,2,3,3,3), ], COL[c(1,2,3,1,2,3,1,2,3), ] ) mat2 <- expand.grid(cn = rownames(COL), rn = rownames(ROW)) row.names(mat1) <- paste(mat2[,2],mat2[,1]) # 行と列の内積 Ip <- mat1[,1] * mat1[,3] + mat1[,2] * mat1[,4] # 指標化残差のベクトル化 Iv <- I |> t() |> as.vector() cor(Ip, Iv) ## [1] 0.9444723
非対称プロット(列主座標)
相関係数1.00。完全に一致します。
COL <- standard.coordinates.columns ROW <- principal.coordinates.rows mat1 <- cbind( ROW[c(1,1,1,2,2,2,3,3,3), ], COL[c(1,2,3,1,2,3,1,2,3), ] ) mat2 <- expand.grid(cn = rownames(COL), rn = rownames(ROW)) row.names(mat1) <- paste(mat2[,2],mat2[,1]) # 行と列の内積 Ip <- mat1[,1] * mat1[,3] + mat1[,2] * mat1[,4] # 指標化残差のベクトル化 Iv <- I |> t() |> as.vector() cor(Ip, Iv) ## [1] 1
対称バイプロット
こちらも相関係数1.00。完全に一致します。
COL <- sympc.coordinates.columns ROW <- sympc.coordinates.rows mat1 <- cbind( ROW[c(1,1,1,2,2,2,3,3,3), ], COL[c(1,2,3,1,2,3,1,2,3), ] ) mat2 <- expand.grid(cn = rownames(COL), rn = rownames(ROW)) row.names(mat1) <- paste(mat2[,2],mat2[,1]) # 行と列の内積 Ip <- mat1[,1] * mat1[,3] + mat1[,2] * mat1[,4] # 指標化残差のベクトル化 Iv <- I |> t() |> as.vector() cor(Ip, Iv) ## [1] 1
大きな集計表で再確認
tarotanさんの記事には
カテゴリー数が少ないのであれば,わざわざ単純対応分析をする必要はないと思う
と書かれています。
それでは大きな集計表で再確認してみましょう。
日経リサーチさんの解説のデータを引用させてもらいます。
18ブランド、20属性の集計表です。
ブランド名はアルファベットに置き換えました。
dat.nr <- c( 18, 43, 175, 249, 52, 133, 78, 34, 93, 40, 207, 165, 108, 35, 78, 23, 115, 97, 30, 52, 124, 248, 59, 29, 48, 19, 113, 75, 165, 161, 24, 25, 47, 177, 36, 126, 16, 38, 21, 11, 36, 48, 101, 97, 86, 63, 50, 57, 50, 54, 58, 35, 43, 63, 42, 45, 37, 53, 32, 49, 51, 284, 26, 15, 7, 6, 52, 11, 110, 144, 10, 17, 27, 118, 20, 87, 8, 9, 4, 10, 284, 7, 452, 188, 76, 25, 177, 223, 181, 19, 156, 39, 272, 86, 52, 85, 28, 85, 185, 318, 60, 2, 265, 100, 72, 55, 64, 66, 33, 10, 115, 45, 111, 20, 32, 12, 39, 48, 62, 123, 85, 4, 329, 132, 79, 51, 94, 105, 67, 27, 118, 32, 121, 47, 32, 42, 25, 72, 94, 182, 189, 40, 233, 36, 27, 16, 80, 176, 107, 19, 57, 24, 88, 73, 13, 67, 7, 49, 89, 104, 106, 112, 87, 20, 16, 11, 63, 60, 55, 65, 24, 10, 43, 69, 10, 43, 8, 31, 38, 26, 37, 297, 31, 23, 14, 14, 60, 20, 102, 94, 24, 14, 19, 87, 26, 71, 4, 21, 6, 10, 148, 28, 197, 46, 25, 21, 70, 151, 80, 10, 78, 22, 67, 55, 16, 53, 12, 43, 73, 73, 77, 100, 159, 81, 32, 26, 118, 125, 126, 22, 110, 25, 81, 77, 29, 78, 15, 79, 48, 45, 352, 40, 253, 18, 24, 13, 125, 203, 164, 111, 30, 22, 177, 184, 12, 98, 14, 79, 119, 152, 24, 240, 58, 120, 44, 117, 95, 18, 125, 87, 76, 88, 69, 55, 96, 67, 161, 61, 17, 24, 42, 16, 149, 42, 41, 38, 30, 37, 13, 8, 58, 30, 49, 18, 10, 12, 28, 29, 28, 43, 168, 121, 140, 75, 50, 35, 140, 97, 184, 98, 39, 25, 88, 157, 30, 153, 57, 68, 64, 77, 72, 155, 106, 43, 25, 27, 64, 42, 113, 59, 49, 19, 48, 77, 13, 71, 18, 48, 39, 36, 49, 155, 74, 24, 34, 27, 59, 35, 64, 63, 27, 17, 28, 66, 20, 47, 18, 30, 23, 18 ) |> matrix( nrow = 18, byrow = TRUE, dimnames = list( Brands = LETTERS[1:18], Attributes = c( "伝統や格式を重んじる", "庶民的", "価格が高い", "流行を作り出している", "価値上昇", "新鮮味", "顧客の心つかんでいる", "気品を感じさせる", "ファン層幅広い", "機能性重視", "デザイン重視", "既成概念囚れない", "存在感", "ずっと付合っていける", "社会動きに敏感", "誰からも好かれる", "躍動感", "さりげなく特徴をアピール", "豊かな気持ちにさせる", "自慢になる" ) ) )
同時布置図ですが、カテゴリ数が多いので矢印は行(ブランド)のみに引いています。
res.ca <- ca(dat.nr) p1 <- fviz_ca(res.ca, map = "symmetric", arrows = c(TRUE, FALSE), title="フレンチプロット") + scale_y_continuous(limits = c(-1.25, 0.75)) + scale_x_continuous(limits = c(-1.25, 0.75)) p2 <- fviz_ca(res.ca, map = "colprincipal", arrows = c(TRUE, FALSE), title="非対称プロット(列主座標)") + scale_y_continuous(limits = c(-2.5, 1.5)) + scale_x_continuous(limits = c(-2.5, 1.5)) p3 <- fviz_ca(res.ca, map = "symbiplot",arrows = c(TRUE, FALSE), title="対称バイプロット") + scale_y_continuous(limits = c(-1.75, 1.0)) + scale_x_continuous(limits = c(-1.75, 1.0)) p1 + p2 + p3 + plot_layout(ncol = 2) + plot_annotation(title = "同時布置図の座標比較")

結論(再掲)
- コレスポンデンス分析の同時布置図を描くときは、対称バイプロットがおすすめです。
- 指標化残差を正確に角度として表現できて、なおかつ見やすいので。
- 従来の同時布置図はフレンチプロットが多いと思いますが、正確でないのであえて選ぶ理由はありません。
- ただ、「だいたい合ってる」ので、角度で読む分には大きく間違えることはなさそうです。
- 縦横のスケールを合わせるのが大前提です。
- そうしないと見かけ上の角度が歪んでしまいます。
参考リンク
Understanding the Math of Correspondence Analysis
Normalization and Scaling in Correspondence Analysis
対応分析のグラフを適切に解釈する条件 : Standard Coordinate, Principal Coordinate を理解する
コレスポンデンス分析の同時布置図は本当に使えないのか?
はじめに
松本健太郎さんの「マーケティングリサーチで使われるコレスポンデンス分析について調べてみた」という記事が書かれたころからでしょうか、コレスポンデンス分析(以下、コレポン)の同時布置図に対する否定的な意見をよく目にするようになりました。
松本さんの議論は
どの年代で見ても20代の購入量は圧倒的なのです。そのような見方は、数量で見れば違和感を覚えます。
という疑問をきっかけに
コレスポンデンス分析は、それぞれ行得点・列得点を算出しているだけで、それらを重ね合わせたに過ぎません。 つまり列要素と行要素との距離は、数理的に定義されず「近い」「似ている」のように解釈できないのです。
というところから
コレスポンデンス分析は行・列をごっちゃにして分析しない。
という結論に至っています。
この記事に対する反響も大きく、Twitterでも同調する意見に多くの「いいね」が付いています。
マーケティングリサーチで使われるコレスポンデンス分析について調べてみた|松本健太郎 @matsuken0716|note(ノート) https://t.co/PnHq6hSYC5
— 松本健太郎 (@matsuken0716) 2019年6月10日
ポジショニングで盛り上がっているので便乗しますが、「イメージ項目」と「ブランド」を同時にプロットした「コレスポンデンス分析」とやらを、調査会社の皆さんには早く根絶していただけると、僕の仕事のひと手間が省けて嬉しいですw
— 高橋孝之|ホジョセン (@inyuinyu) 2021年1月24日
松本さんが完結にまとめてくれてます。https://t.co/W1QHqe0KUB
私は統計の専門性低いので細部の理解は怪しいですが、弊社内では「コレポンはそれっぽく理解した気になるだけでミスリードもあり使えない」という扱いになってますね。
— 山口義宏 𝑰𝒏𝒔𝒊𝒈𝒉𝒕𝒇𝒐𝒓𝒄𝒆 (@blogucci) 2022年1月3日
マーケティングリサーチで使われるコレスポンデンス分析について調べてみた|松本健太郎 @matsuken0716 https://t.co/7j6IHiMEw7
松本さんの問題提起より前からコレポンの同時布置図の解釈について否定的な意見は散見されました。 例えば朝野先生による解説でも
行要素と列要素を別々の散布図に書くというグラフィック表現が手堅い対応でしょう。
と結論付けらえています。
確かにコレポンの誤った解釈は時折目にしますし、調査会社のサイトにある手法説明にも誤ったものを見かけます。
本当にコレポンの同時布置図は使ってはいけないようなものなのでしょうか?
しかし、実務で何十枚もコレポンの同時布置図を描いてきた者としては疑問符が浮かびます。
「それって、同時布置図の正しい解釈を知らないだけじゃないの???」
結論
先に私の結論を書きます。
- コレポンの同時布置図において集計表の行と列の関係は角度の大きさで解釈できるよ
- コレポンの同時布置図が表現しようとしているのは割合の残差であり、残差の大きさは原点から引いた各点がなす角度の大きさとして表現されるよ。
- コレポンは実数の大きさには関心がないよ。
- 残差の大きさが角度の大きさとして表される描画方法を使わないとダメだよ。
- 原点から各点へ矢印を引くと解釈しやすいよ。
- 縦横のスケールは合わせないとダメだよ。
- 縦横の軸の意味を解釈しようとするのはダメだよ。
- 点と点の距離で関係の強さを解釈しようとするのはダメだよ。
解説
ここからRを用いて説明をすすめます。
サンプルデータ
松本さんと同じデータを使うのが本当ならいいんでしょうが、松本さんのデータには馬蹄形問題が潜んでいて、話が若干ややこしくなります。
なので、今回はコレポンの話に絞るためにこちらのデータを使います。 これは架空のブランドのブランドイメージ調査のデータになっています。
サンプルデータを用意します。
(dat <- c(5, 18, 19, 12, 3, 7, 46, 29, 40, 7, 2, 20, 39, 49, 16) |> matrix( nrow = 5, dimnames = list( Brands = c("Butterbeer", "Squishee", "Slurm", "Fizzy Lifting Drink", "Brawndo"), Attributes = c("Tasty", "Aesthetic", "Economic") ) )) ## Attributes ## Brands Tasty Aesthetic Economic ## Butterbeer 5 7 2 ## Squishee 18 46 20 ## Slurm 19 29 39 ## Fizzy Lifting Drink 12 40 49 ## Brawndo 3 7 16
コレポンの実行
まずはとにかくコレポンを実行してみましょう。
Rでコレポンを実行するパッケージは複数ありますが、今回はデータの取り出しやすさからcaパッケージのca()関数を使用します。
library(ca) res.ca_ca <- ca(dat) summary(res.ca_ca) ## ## Principal inertias (eigenvalues): ## ## dim value % cum% scree plot ## 1 0.070369 84.5 84.5 ********************* ## 2 0.012892 15.5 100.0 **** ## -------- ----- ## Total: 0.083260 100.0 ## ## ## Rows: ## name mass qlt inr k=1 cor ctr k=2 cor ctr ## 1 | Bttr | 45 1000 190 | -549 854 192 | -227 146 180 | ## 2 | Sqsh | 269 1000 378 | -333 948 425 | 78 52 126 | ## 3 | Slrm | 279 1000 92 | 81 237 26 | -145 763 452 | ## 4 | FzLD | 324 1000 153 | 173 759 138 | 97 241 239 | ## 5 | Brwn | 83 1000 186 | 431 997 220 | -24 3 4 | ## ## Columns: ## name mass qlt inr k=1 cor ctr k=2 cor ctr ## 1 | Tsty | 183 1000 242 | -254 585 168 | -214 415 649 | ## 2 | Asth | 413 1000 256 | -202 790 239 | 104 210 348 | ## 3 | Ecnm | 404 1000 502 | 321 999 593 | -10 1 3 |
そして、同時布置図を描きます。
いろいろオプションが付いたり、見慣れない矢印があったりしますがいったんこのまま進めます。
res.biplot_symbiplot <- plot(res.ca_ca, map = "symbiplot", arrows = c(TRUE, TRUE), xlim = c(-1.1, 0.9), ylim = c(-1.1, 0.9), main = "ca - Biplot - symbiplot")

各点の座標は以下のようになっています。
res.biplot_symbiplot ## $rows ## Dim1 Dim2 ## Butterbeer -1.0665778 -0.67407378 ## Squishee -0.6468361 0.23054640 ## Slurm 0.1563567 -0.42910993 ## Fizzy Lifting Drink 0.3359331 0.28929206 ## Brawndo 0.8359247 -0.06979996 ## ## $cols ## Dim1 Dim2 ## Tasty -0.4937814 -0.63528783 ## Aesthetic -0.3915076 0.30897357 ## Economic 0.6242065 -0.02893797
ちなみにfactoextraパッケージのfviz_ca()を使うとggplot2ベースの同時布置図も描けます。
library(factoextra) fviz_ca(res.ca_ca, map = "symbiplot", arrows = c(TRUE, TRUE), title = "CA - Biplot - symbiplot") + scale_x_continuous(limits = c(-1.1, 0.9)) + scale_y_continuous(limits = c(-1.1, 0.9))

指標化残差
さて、先に「コレポンの同時布置図が表現しようとしているのは割合の残差」と書きました。
ここでいう残差(residual)とは「実測値と期待値の差」を意味します。
クロス集計表における残差分析の残差と同じです。
今回のデータの残差を計算してみましょう。
総度数nを算出
(n <- sum(dat)) ## [1] 312
観測割合P(observed proportions、各セルの度数を総度数で割った値、同時確率分布)を算出
(P <- dat / n) ## Attributes ## Brands Tasty Aesthetic Economic ## Butterbeer 0.016025641 0.02243590 0.006410256 ## Squishee 0.057692308 0.14743590 0.064102564 ## Slurm 0.060897436 0.09294872 0.125000000 ## Fizzy Lifting Drink 0.038461538 0.12820513 0.157051282 ## Brawndo 0.009615385 0.02243590 0.051282051
行質量(row masses, 行周辺確率分布)と列質量(column masses, 行周辺確率分布)を算出
(row_masses_pi <- rowSums(P)) ## Butterbeer Squishee Slurm Fizzy Lifting Drink ## 0.04487179 0.26923077 0.27884615 0.32371795 ## Brawndo ## 0.08333333
(col_masses_pj <- colSums(P)) ## Tasty Aesthetic Economic ## 0.1826923 0.4134615 0.4038462
期待割合E(Expected proportions)を算出
(E <- row_masses_pi %o% col_masses_pj) ## Tasty Aesthetic Economic ## Butterbeer 0.008197732 0.01855276 0.01812130 ## Squishee 0.049186391 0.11131657 0.10872781 ## Slurm 0.050943047 0.11529216 0.11261095 ## Fizzy Lifting Drink 0.059140779 0.13384492 0.13073225 ## Brawndo 0.015224359 0.03445513 0.03365385
残差R(Residuals)を算出
(R <- P - E) ## Attributes ## Brands Tasty Aesthetic Economic ## Butterbeer 0.007827909 0.003883136 -0.01171105 ## Squishee 0.008505917 0.036119329 -0.04462525 ## Slurm 0.009954389 -0.022343442 0.01238905 ## Fizzy Lifting Drink -0.020679241 -0.005639793 0.02631903 ## Brawndo -0.005608974 -0.012019231 0.01762821
残差は集計表の行と列のカテゴリ間に関係がないという仮定のもとで期待される値(E、期待値、期待割合)と実際に観測された値(P、観測値、観測割合)の差です。
残差の絶対値が大きいと期待値とズレている、すなわち行と列のカテゴリ間に何らかの関係がありそう、ということになります。
クロス集計表の残差分析と基本的な考え方は同じですが、クロス集計表の残差分析が生の度数の残差を分析するのに対して、コレスポンデンス分析が分析するのは割合の残差であるところが異なります。
生の残差は各カテゴリの度数に左右されるため、期待値で割って正規化します。
これを指標化残差I(Indexed residuals)と呼びます。
(I <- R / E) ## Attributes ## Brands Tasty Aesthetic Economic ## Butterbeer 0.9548872 0.20930233 -0.6462585 ## Squishee 0.1729323 0.32447398 -0.4104308 ## Slurm 0.1954023 -0.19379845 0.1100164 ## Fizzy Lifting Drink -0.3496613 -0.04213677 0.2013201 ## Brawndo -0.3684211 -0.34883721 0.5238095
指標化残差が0.955であれば、観測値は期待値より95.5pt高いということを意味します。
P/E ## Attributes ## Brands Tasty Aesthetic Economic ## Butterbeer 1.9548872 1.2093023 0.3537415 ## Squishee 1.1729323 1.3244740 0.5895692 ## Slurm 1.1954023 0.8062016 1.1100164 ## Fizzy Lifting Drink 0.6503387 0.9578632 1.2013201 ## Brawndo 0.6315789 0.6511628 1.5238095
この指標化残差を可視化するのがコレポンの同時布置図のねらいです。
コレポンにおける指標化残差の表現
コレポンの同時布置図において、行の点Aの座標を(x1, y1)、列の点Bの座標を(x2, y2)とすると、x1 * x2 + y1 * y2が指標化残差と一致します。
例えばtastyとButterbeerの指標化残差は0.955。
先に描いたコレポンの同時布置図でのそれぞれの座標は、tastyが(-0.494, -0.635)、Butterbeerが(-1.067, -0.674)。
上記の計算をすると0.955で指標化残差と一致します。
res.biplot_symbiplot$rows[1, 1] * res.biplot_symbiplot$cols[1, 1] + res.biplot_symbiplot$rows[1, 2] * res.biplot_symbiplot$cols[1, 2] ## [1] 0.9548872
つまり、コレポンの同時布置図上でtastyとButterbeerの内積が指標化残差を表現できていることが分かります。
内積によって、2つのベクトルがなす角度も定まるので、 バイプロット上でtastyとButterbeerのベクトルがなす角度が標準化残差を表している。といえます。
次に、原点からの距離に注目します。
(dist_Butterbeer <- sqrt((0 - res.biplot_symbiplot$rows[1, 1])^2 + (0 - res.biplot_symbiplot$rows[1, 2])^2)) ## [1] 1.26173
(dist_Tasty <- sqrt((0 - res.biplot_symbiplot$cols[1, 1])^2 + (0 - res.biplot_symbiplot$cols[1, 2])^2)) ## [1] 0.8046184
今度は2つのベクトルの角度を算出します。
library(Morpho) Butterbeer <- as.matrix(c(res.biplot_symbiplot$rows[1, 1], res.biplot_symbiplot$rows[1, 2])) Tasty <- as.matrix(c(res.biplot_symbiplot$cols[1, 1], res.biplot_symbiplot$cols[1, 2])) (Butterbeer_Tasty_angle <- angle.calc(Butterbeer, Tasty) / pi * 180) ## [1] 19.85088
ここでAのベクトルの長さ*Bのベクトルの長さ*cos(AとBのなす角度)が指標化残差と一致します。
dist_Butterbeer * dist_Tasty * cos(Butterbeer_Tasty_angle * pi / 180) ## [1] 0.9548872
やはり、2つのベクトルがなす角度が、行と列の2つのカテゴリの指標化残差を表せています。
注目したいのはこの式の最初の2つの部分が、ベクトルの長さになっていることです。
つまり、原点からの距離が遠い点ほど、その点ともう一方の点との関連が強くなることを表しています。
注意!
ここまでで、コレポンの同時布置図が行と列のカテゴリ間の関連を適切に表現できていることに納得いただけたかと思います。
ただし、ここでいくつか注意すべき点があります。
同時布置図を描く方法によって、これらの法則が保たれない場合があるのです。
caパッケージのplot.ca()やfactoextraのfviz_ca()のmapオプションで方法を指定できますが、指標化残差を角度やベクトルの長さで表現できるのは"colprincipal"、"rowprincipal"、"symbiplot"の三つです。
デフォルトの"symmetric"や他の方法ではこの法則が保たれません。
まとめ
コレポンの同時布置図は、2つのグループ(今回のサンプルデータではブランドと属性)の間およびグループ内の相対的な関係を分析するために使用されます。
コレポンは、相対的な関係しか表しません。
実数の大きさは元の集計表で確認しましょう。コレポンでは表現されません。
原点から離れれば離れるほど、より特徴的になります。原点に近いほど偏りがないことになります。
縦横のスケールを合わせること。そうしないと見かけ上の角度が歪んでしまいます。
さいごに
ここで、再び松本さんの記事へ立ち戻りましょう。
どの年代で見ても20代の購入量は圧倒的なのです。そのような見方は、数量で見れば違和感を覚えます。
それはコレポンが相対的な関係を表すもので、実数を表すものではないからです。
コレスポンデンス分析は、それぞれ行得点・列得点を算出しているだけで、それらを重ね合わせたに過ぎません。 つまり列要素と行要素との距離は、数理的に定義されず「近い」「似ている」のように解釈できないのです。
行と列の点の距離で関係を論じられないのはその通りですが、ベクトルの角度と長さによって指標化残差としてそれは表現されています。
コレスポンデンス分析は行・列をごっちゃにして分析しない。
これはさすがに「羹に懲りて膾を吹く」というものです。
コレポンの同時布置図は正しく描いて、正しく解釈すればクロス集計表を解釈する上での強力な道具になりえます。
松本さんのデータをこれまで説明したやり方で同時布置図にするとこうなります。
drink <- c( 1025, 270, 331, 270, 81, 6233, 1618, 1155, 667, 180, 1318, 389, 309, 229, 70, 1209, 219, 239, 349, 200, 5167, 769, 797, 1121, 646 ) |> matrix( nrow = 5, byrow = TRUE, dimnames = list( 銘柄 = c("生茶", "伊右衛門", "綾鷹", "十六茶", "お~いお茶"), 年代 = c("20代", "30代", "40代", "50代", "60代") ) ) drink |> ca() |> fviz_ca( map = "symbiplot", arrows = c(TRUE, TRUE), title = "Drink") + scale_x_continuous(limits = c(-1.5, 0.75)) + scale_y_continuous(limits = c(-1.25, 1))

ここから解釈できるのは、
- 20代は原点に近くブランドの選好に相対的な特徴は見られない。全体におけるブランドの割合と大きな差がない。
- 40代は「生茶」が全体と比べて相対的に多く選ばれている。
- 60代は「お~いお茶」や「十六茶」が全体と比べて相対的に多く選ばれている。
といったところでしょうか。
繰り返しになりますが、コレポンは実数には関心がないので、そこはモザイクプロットなどで観察しましょう。
そもそも、20代が6割を占めているデータなので、20代が「全体におけるブランドの割合と大きな差がない」のも当然ですね。
library(vcd) drink |> t() |> mosaic(shade=TRUE, legend=TRUE, main="drink", direction="v")

お疲れ様でした。
追記:続きを書きました。
参考リンク
Understanding the Math of Correspondence Analysis
How to Interpret Correspondence Analysis Plots (It Probably Isn’t the Way You Think)
Correspondence Analysis: What is it, and how can I use it to measure my Brand? (Part 1 of 2)
Correspondence Analysis: What is it, and how can I use it to measure my Brand? (Part 2 of 2)
CA - Correspondence Analysis in R: Essentials
